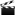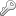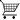.
O P E N A C C E S S S O U R C E : Mechanisms of Ageing and Development
Highlights
• Machine learning offers a set of tools that are making significant contributions towards our understanding of the complex relationships between diseases.
• More advanced models take a range of modalities from large routine or research datasets into account with little data pre-processing or information loss at study design stage.
• Recent methodological developments such as matrix factorisation, deep learning and topological data analysis show promising potential for better understanding of evolving patterns of multimorbidity.
Abstract
The prevalence of multimorbidity has been increasing in recent years, posing a major burden for health care delivery and service. Understanding its determinants and impact is proving to be a challenge yet it offers new opportunities for research to go beyond the study of diseases in isolation. In this paper, we review how the field of machine learning provides many tools for addressing research challenges in multimorbidity. We highlight recent advances in promising methods such as matrix factorisation, deep learning, and topological data analysis and how these can take multimorbidity research beyond cross-sectional, expert-driven or confirmatory approaches to gain a better understanding of evolving patterns of multimorbidity. We discuss the challenges and opportunities of machine learning to identify likely causal links between previously poorly understood disease associations while giving an estimate of the uncertainty on such associations. We finally summarise some of the challenges for wider clinical adoption of machine learning research tools and propose some solutions.
1. Introduction
Advances in medicine have led to an increase in life expectancy and reduction of major disabilities. These achievements have also contributed to the rise in chronic conditions (that are more prevalent in older ages) and their co-occurrence, a phenomenon known as multimorbidity, that is, the simultaneous presence of two or more chronic conditions in the same individual) (The Academy of Medical, 2018). Indeed, research has shown that the proportional increase in multimorbidity over the past few years is only partially explained by population ageing, stressing its relevance to young and middle-aged adults (Fig. 1).

Fig. 1. Annual crude and age/sex-standardised prevalence of number of comorbidities in incident cardiovascular disease patients (credits to Tran et al. (2018)); Number labels for each line refer to the number of comorbidities. (A) Crude prevalence. (B) Age/sex-standardised prevalence.
Medical research commonly focuses on the study of diseases – and their prevention and management – in isolation. Many such conventional approaches are likely to remain relevant to narrower questions relating to multimorbidity and testing of specific hypotheses, but are unlikely to be sufficient to answering questions relating to clustering of multiple diseases and their interactions as an important step towards identification of strategies for their prevention and management (The Academy of Medical, 2018).
Multimorbidity is characterised by a high degree of complexity arising from the presence of multiple diseases, their biological and non-biological determinants and consequences, and multiple interactions over time. Although such complexities are not unique to multimorbidity, they have not been sufficiently leveraged or embraced in prior research in the field. For instance, most previous studies of multimorbidity have been cross-sectional, which renders them unsuitable for the investigation and characterisation of how a disease progresses over time, taking into account how the trajectory interacts with its broader context (e.g., presence of other diseases, use of medications, and, more broadly, a patient’s entire medical history). Studies have often been based on small samples sizes or have focused on a small subset of conditions, hampering their ability to mine the disease clusters and phenotypes that are less frequent and, hence, poorly understood (The Academy of Medical, 2018). Thus, the complex temporal dynamics of multiple interactions inherent to multimorbidity has highlighted the importance of employing alternative methods that are better suited for tackling this complexity.
Outside multimorbidity research, one can draw parallels to the growing number of studies that aim to discover and characterise the so called “computable phenotypes” (Bennett et al., 2017), using various modalities of medical data that go beyond diagnoses, and considering additional information such as medications, interventions, physical measurements, and laboratory results. Most such studies aim to help the emerging field of precision medicine with the optimal care pathway for patients, based on their stratification into population subgroups that they have derived. Although faced with the similar challenge of complexity, the key difference to multimorbidity research is that such deep phenotyping studies have been aiming to define more homogeneous groups among patients with the same single diagnosis. Viewed from this perspective, the study of multimorbidity could be diagnosis-wide phenotyping, when multiple diseases within the same individual are considered simultaneously, or as comprehensive multi-modal phenotyping, when in addition to multiple diseases, information about the broader context in which diseases occur is also taken into account. In other words, complex multimorbidity modelling would ideally consider the entire medical history of an individual into account in an effort to reveal hidden patterns within the population without necessarily starting with a single condition.
Of course, the comprehensive discovery of such phenotypic classes (including, but not limited to multimorbidity classes) and their translation into clinical care, will depend on a number of constraints and choices – from study design and data availability, to the computational paradigms (or models) employed by researchers. In recent years, rapid developments in machine learning (ML), including deep learning (DL), have led to outstanding results (and at times superhuman performance) in previously difficult tasks, such as autonomous driving (El Sallab et al., 2020), machine translation (Devlin et al., 2018), computer vision (He et al., 2016), strategic decision making (Silver et al., 2017), and in domains with vast search spaces (Chen et al., 2016). Despite their relatively recent adoption in healthcare, ML methods have started to show promising results in drug discovery and development (Ekins et al., 2019), large-scale gene expression profiling (Chen et al., 2016) histopathological diagnosis (Litjens et al., 2016), brain MRI segmentation (Akkus et al., 2017), and disease prediction using electronic health records (EHR) (Ayala Solares et al., 2020; Hassaine et al., 2019; Li et al., 2020) (readers are referred to (Rajkomar et al., 2019) for a more comprehensive review of ML in medicine).
Given the importance of methodology in multimorbidity research, and the latest developments in the field of machine learning, this paper aims to review the state of relevant methodology and introduce some of the latest ML developments that have the potential to further advance this field. We will start in Section 2 by describing some of the key methodologies that have been employed for the study of multimorbidity (e.g., those that are based on network analysis and matrix/tensor factorisation). In section 4 we describe some of the methodological challenges and suggest potential solutions for them. In section 4 we will introduce some of the recent advances in matrix and tensor factorisation, deep learning, and topological data analysis. Despite their high potential for impact meaningful contribution to in the field, these latter methods have not yet been employed and evaluated for multiformbidity research. We will then conclude with summary of the approaches presented and suggestions for future research.
2. Current state of methodology
The field of multimorbidity research has already seen the use of a wide range of techniques for mining multimorbidity patterns - from network modelling, to probabilistic models and matrix (and tensor) factorisation techniques. This section provides an overview of how these methods have been applied in multimorbidity research.
2.1. Pairwise methods
Some of the earlier research using this method take an approach by initially assessing diseases as pairs and then combining the results across a wider range of diseases. In the pairwise class of techniques, disease pairs that show co-occurrence frequencies that are higher than their predicted individual frequencies in the population, are considered to be “connected”. In one of the early works in this category, Hidalgo et al. (2009) built a disease network in which the nodes and edges represented diseases and their connectivity, respectively. To overcome the challenge of missing temporal information in the resulting network, the authors carried out correlation analyses to decide whether a node property spreads along the links of the network and modelled how diseases propagate over time through the network. In another landmark study, Jensen at al. (Jensen et al., 2014) proposed a temporal disease network in order to provide pairwise methods with the ability to explicitly deal with time. In this approach, each edge represented a pairwise connectivity plus the time difference between the incidence of diseases that the edge connects. In a similar approach, Giannoula et al. (2018) used the pairwise connectivity plus the disease-timing data to cluster the diseases using dynamic time warping. The use of pairwise methods for mining multimorbidity patterns and phenotyping was not limited to disease data alone. (Goh et al. (2007) built a bipartite graph of genes and diseases, as a framework for the study of phenotype- and disease-gene associations.
While pairwise methods are valuable in generating comorbidity hypotheses for disease pairs, their inability to address conditional probabilities of multiple diseases directly (Pearl, 2009) can make the resulting multi-disease networks potentially misleading.
2.2. Probabilistic methods
Another class of models that have been employed for mining multimorbidity patterns can be referred to as “probabilistic methods”. Instead of simply looking at pairs of diseases, these methods provide a wholistic view of the relationships among diseases. For instance, (Strauss et al. (2014)) applied latent class growth modelling to a small UK EHR dataset, to identify clusters of multimorbidity trajectories. The authors clustered patients based on how many chronic conditions they developed over time, into 4 different groups ranging from no recorded chronic problems to increasing number of chronic morbidities. Although this work provided important insights about the accumulating number of diseases over time, it was not designed to assess the temporal relationships of diseases with each other or other patient covariates, which is a key aspect in the study of multimorbidity. Another approach to modelling multimorbidity trajectories is the use of computationally intensive Hidden Markov Models. Such models can learn progression of an individual’s health trajectory while incorporating time as a continuous variable. In an early example, (Wang et al. (2020a)) applied this method to patients with chronic obstructive pulmonary disease and showed how different patient groups developed additional comorbidities over time. The discovery of such distinct trajectories, as the authors argued, could assist decision makers to better understand the heterogeneity in disease progression and help researchers to potentially identify more targeted interventions. Although focused on the progression of a single disease, the modelling approach could potentially be applied for analysis of multiple disease trajectories over time.
2.3. Factorisation methods
Factorisation methods have seen a growing popularity in many fields including the study of multimorbidity. They have been extensively used to extract latent factors in many domains including image segmentation (Zhang et al., 2019) recommender systems (Abdi et al., 2018) and finance (Sun et al., 2016). Factorisation assumes that each patient’s medical record is the result of combining multiple “underlying factors” that are common across the population; the variability from one patient to another is due to the extent to which such factors are expressed in each patient, at each time/age. A factor can be thought of as a unique combination of concepts (such as diagnoses and medications) that can be found in EHR; for example, while one factor can denote ophthalmological disorders, another might be hypertensive diseases, and in patients with diabetes, both factors are likely to show a high expression. Factorisation allows the reduction of the multiple individual diseases or other features into a smaller set of factors that can explain the correlation between them.
In one of the simplest forms of these approaches, one starts by representing the data using a matrix D, where patients and diseases are the two dimensions: D(i,j) = 1 if patient i had disease j at some point in their life, and D(i,j) = 0 otherwise. The factorisation is the process of decomposing D into two matrices A and B such that R aprox. = A x B. The rank R, which is equal to the number of columns in A and the number of rows in B, is generally set through search and optimisation or based on empirical evidence. B is usually called the basis matrix, where each row r represents the belonging of every disease to the r’th component (i.e., the r’th disease cluster, or disease-based phenotype). A, on the other hand, is called the mixing matrix, it shows how a linear combination of R clusters that can explain the diagnoses for each and every patient (see Fig. 2.a for an illustration).

Fig. 2. Two common types of factorisation methods employed in the multimorbidity literature; (a) Matrix factorisation, and (b) Tensor factorisation. Note that, one can change the concept that each dimension represents; in these illustrations, we show a very common way of choosing the dimensions.
This family of methods have seen a growing popularity in the field, as unlike previously described methods, they do not require much expert knowledge and hence have the potential to lead to novel discoveries. In addition, they are capable of incorporating a large set of information and different modalities at the same time. In one study, for instance, Holden et al. (2011) and (Kirchberger et al. (2012) applied matrix factorisation to extract multimorbidity patterns from self-reported diagnoses. Schäfer et al. (2010) applied factor analysis to extract multimorbidity patterns of elderly patients. Similar studies have also been proposed on different datasets, such as the work of Roso-Llorach et al. (2018) who concluded that clusters of diseases obtained from an older patient cohort with multimorbidity using hierarchical cluster analysis and exploratory factor analysis were not always similar. The authors suggested factor analysis to be more useful for analysing multimorbidity patterns whereas hierarchical cluster analysis (a more conventional statistical approach that assigns diseases to different clusters) could serve in generating new hypotheses for inter-cluster and intra-cluster associations.
The aforementioned factorisation studies only considered diseases when forming D, and hence cannot untangle the relationships that other clinical concepts (such as medications, procedures, or lab tests) could have on the natural history of the disease. In an attempt to alleviate such issues, Ho et al. proposed to add procedures as a third dimension (Ho et al., 2020), and Wang et al. added medications (Wang et al., 2020b); this process will change the problem from matrix factorisation (i.e., with a 2D input) to tensor factorisation (i.e., with a 3D input) – see Fig. 2.b for an illustration.
The methods described above produced factors that show disease-disease associations, as well as associations among diseases and other clinical concepts (such as medications and procedures), but as they did not account for temporal evolution of these factors over time, their clinical usability remains somewhat limited.
2.4. Temporal phenotyping
To account for the temporal aspects of multimorbidity, Zhou et al. (2020) represented each patient’s EHR using a matrix, where the two dimensions were diagnoses and time. One of the strengths of their approach is its ability to handle missing data, which is common in EHR. The authors showed that the obtained phenotypes are useful in predicting the onset of new diseases, such as congestive heart failure or end stage renal disease. However, the clinical relevance of the derived phenotypes remains uncertain. In a different approach, Perros et al. (2019) considered the chronological order of encounters (as opposed to the time/age at which they actually happened). Their method has recently been extended by Afshar et al. (2019) to jointly account for dynamic and static information (such as demographics information). The authors showed that this method produces clinically meaningful phenotypes that yielded accurate heart failure prediction, but given that the intervals between two consecutive encounters can contain important medical information and vary greatly from patient to patient (and even for the same patient), explicitly accounting for the time in these methods – as opposed to order – can be a natural improvement.
In another study, (Zhao et al. (2019)) incorporated the time to the onset of cardiovascular disease as a dimension in the tensor. The phenotypes obtained from this approach, while temporally profiled, are specific to cardiovascular disease patients (see Fig. 3.b for an illustration of this method).

Fig. 3. Examples of temporal phenotyping. (a) using a tensor where time is mapped to a dimension, (b) using a tensor where the encounters are mapped to a dimension © using concatenated matrix representations.
.../...
.