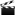Recently, when I visited the Repeat Diagnostics website, I was struck by the
telomere length curves they showed for a couple of their clients. These curves exhibit two notable features.
(1) There's a standard telomere length curve
shape that describes how,
on average, everyone's telomeres shorten as a function of time. We lose telomere base pairs the fastest at birth (at a rate of 140 base pairs a year?), with the rate steadily slowing as we work our way through childhood and early adulthood. Somewhere around 55 or 60, there's an inflection point in the curve where the curvature shifts from positive to negative. Our rate of telomere erosion in at its lowest point at that age, with a rate of telomere loss of about 35-36 base pairs a year. (The curve is nearly flat from 40 to 70, with telomere loss rate <40 base pairs per year.) After the age of 70, the curve begins to fall ever faster.
(2) There are wide variations in the initial lengths of people's chormosomes at birth. This dispersion of individual telomere lengths at birth looks as though it might be Gaussian, with a standard deviation of, maybe, 1,000 base pairs. If so, the 90th and 10th percentiles are about ±1.27 standard deviations from the mean, and the 99th and 1st percentiles would be about ±2.06
s. This means that about 1 in 10 of us are born with telomeres with a median telomere length about 11,700 base pairs long, and 1 in 100 of us are bequeathed telomeres with a median extension of about 12,500 base pairs. One in 700 of us would greet the world with about 13,400 base pairs.
Averaged over populations these telomere length advantages remain unchanged throughout life!
This may help to explain the scatter on telomere measurement charts. We're, maybe, not looking at fluctuations in telomere lengths over time, but at individual differences in birth date telomere lengths that are conserved throughout life.
A third-degree polynomial (a cubic) is the simplest polynomial fit that can describe this curve. I've fitted a cubic,
Telomere Length (TL) = d - at3 - bt2 - cy, to this curve as best I could by visually guesstimating values from the chart. The coefficients for this polynomial fit for the middle (average) curve are:
a =
9.5833333 = 9 7/12thsb =
-17.25c =
14.0666667 = 14 1/16thd =
10.4 kilobase pairs d is the initial value for the middle (third) curve, and it appears to be somewhere in the neighborhood of 10,400 base pairs for the average person at birth.
To keep these numbers moderate, I measured time as a fraction from 0 to 1, where 1 = 100 years, and I measured telomere lengths in kilobase pairs.
Since the other four curves have identical shapes, they may be modeled by adding or subtracting 1,270 base pairs to "d" to get to the 90th or 10th percentiles, and by adding or subtracting 2,060 base pairs to "d" to accommodate the 99th and 1st percentiles respectively. (a, b, and c would be the same for all five curves.)
The characteristics of this cubic fit curve are that it's anti-symmetric around the inflection, which I took to be 60 for this cubic fit. Differentiating the cubic to get the slope (annual rate of telomere loss) yields:
Rate of telomere change = - 3 at2 - 2 bx - c.
At t = 0,
Rate of telomere change = -c. But c = 14,067 base pairs per century, or 140.67 base pairs per year. So the rate of telomere change at birth for everyone is about:Rate of telomere change = -140.67 base pairs a yearsBecause this is a cubic fit and is anti-symmetric about age 60 (0.6 centuries), the slope at age 120 is equal to the slope at birth:
-140.67 base pairs a years. This is an artifact (limitation) of the model.I'm working a 4th-degree polynomial fit (a quartic) but I haven't finished it yet.
A logical next step would be to contact Repeat Diagnostics to seek more accurate numbers for this curve fit (although high-fidelity numbers may be contingent upon additional data-gathering over larger populations).
It's tempting to relate telomere lengths at birth to life spans, but I think it must be more complicated than that. If you smoke heavily and work in an asbestos factory, I suspect that you may get lung cancer even if you were blessed with long telomeres at birth. Also, identical twin studies suggest ot me a meaningful role for lifestyle choices.