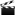a chiral geometry shape that is like a rolling circle with utilizations at nanotechnology

I noticed that a microwave dinner tray sleeve did this thing where it would collapse one direction, yet expand and roll the other direction, then I thought about the geometry as well as varius utilizations

A circular geometric shape that only rotates towards one direction, rather than a parallelogram, which can squish either direction, and is absent rolling I noticed that a quadrilateral tube shaped piece of paper about 90 90 70 110 (not [] just nearly []) would parallelogram flatten at one direction while at the other direction the side would bulge out to a curve stabilizing its height rather than collapsing the parallelogram. So if you were to roll this like a square wheel on a shaped groundbase it would be able to roll only one direction. I thouhgt this was mathematically nifty because from some perspectives conserving puffed up dimension at one direction yet flattening another direction is like an emergent effect of greater dimension yet anisotropic based on something just slightly different from a 90 90 90 90 squarellogram ( [] )which flattens either way. The idea that this could work at a circle or loop of numbers, like a numberline connected to be a circle suggests that simple integer values on a numberline would cause the numberline to roll chirally, just one direction, based only on a group of stated values on a circular numberline. This reminded me of simple machines (like ancient math simple machines) that always do a particular thing. I was reminded of nanotechnology as well as this could be a simplest unidirectional molecular shape, that is it would always travel towards or away from a molecule core like a benzene so is a kind of assembly track to nanotechnology

also thinking about polytopes that go with the regular solids , it could be that at noneuclidean geometries the sides of a 6 or 7 or 8 or nagon could actually meet each other to 360ize forming a regular solid at a slight curved surace, there is the possibility that on a spherical surface there are completely different regular solids and that the physicists that study the shape of the universe could describe other regular solids at the most observationally likely universe shape this could have ngneering function as it is a way to pack space like squares or cubes

youtube comment on video “perfect shapes”n “higher dimension” numberphile
Also with the 5,6,3,3,3, thing it seems strange to presume that higher dimensions would be at euclidean (cartesian) space rather than some other thing (curved or fractal) which would give all of them multiobject contact angles combining to 360, so all of the higher dimensions could have regular solids if they were slightly curved or fractal a kind of nifty way of thinking about this is a mirrored bowl, is there a shape like a mirrored bowl where a sphere would be retroreflectable to have edges that touch (currently tangents) so that all the spheres could combine to make a regular solid or polytope. even those these are actual spheres, there is a noneuclidean geometry where their contact angles are 360 or less, creating a space where a hypersphere is a polytope. This is nifty from an engineering perspective, because the query, how would you slightly reshape space to permit higher dimensional regualr solids could have engneering utility (cubes are packable, other things mick be packable at curved spaces as new polytopes)

at a noneuclidean space there are more than 360 degrees would the 4d icosohedron work if it was at a curved noneuclidean space?

Then a different technology

I read about robotically raised, automated environment research mice, at the article they did not mention big data, sometimes a word for AI pattern sensing. I think that better pharmeceuticals could be